Understanding Quantum Computing

What are quantum computers, how do they work and what they can do that the classical computers can’t? In this post I want to explain some of the most important facts about quantum computing, so if you are interested in this hot topic, please read further.

History of the quantum

More than one hundred years ago a group of best world’s scientists discovered and described quantum phenomena, so I think it is worth mentioning in the beginning of this article their names and contributions:

First, Max Planck spoke in 1900 about light “quanta” in sense that light energy can exist only in discrete packages,
this lead Niels Bohr in 1913 to apply the same principle on energy of electrons in an atom.
In 1926, Erwin Schrödinger and Werner Heisenberg developed independently Wave and Matrix Quantum Mechanics, two unifying mathematical models of atomic quantum phenomena.
The same year, Enrico Fermi described the distribution of particles over energy states, later called Fermi-Dirac statistics
Wolfgang Pauli in 1927 identified how particles interact with external electromagnetic field, and in the end,
Also in 1927, Paul Dirac created quantum field theory

Curiously, Albert Einstein opposed to quantum mechanics, not accepting the randomness of quantum phenomena.

These are basically the fathers of quantum theory who left very rich legacy, recognized nowadays through concepts and terms like Planck’s constant, Copenhagen Interpretation, Heisenberg’s Uncertainty Principle, Schrödinger’s Equation, Fermions, Dirac’s notation, Pauli matrices and others. Those who wish to study this subject deeper will also learn about Hilbert Space, named after mathematician David Hilbert, and Bloch Sphere named after Felix Bloch, two individuals who also contributed substantially to this early development of quantum theory.

After this initial period, physicists were working mostly on experimentation to prove the validity of quantum mechanics postulates and finally in 2015 they resolved all doubts when three independent experiments showed that there is no other explanation for the quantum behaviour of particles like photons and electrons, apart from those provided by the quantum theory.

Quantum Computing in the form of Quantum Information Science was born late 1970’s. The most influential researchers who helped develop this theoretical concept were Paul Benioff, Yuri Manin, Richard Feynmann and David Deutsch. Their main idea was to use quantum phenomena for information processing. Feynmann got famous in 1982 for explaining how a quantum system could be used to do computations and act as a simulator or other physical (quantum) systems.

But maybe the most interesting period started in 1990’s with the development of algorithms, which propelled interest and investments in quantum computing :

Deutsch-Jozsa algorithm in 1992
Schor’s algorithm in 1994 (known to be able to break encryption codes)
Grover’s algorithm in 1996 (database search)

First concrete quantum computers were created in 1998 simultaneously in three labs: Oxford, Almaden (IBM) and Berkeley. These machines were based on nuclear magnetic resonance, but this technology was later abandoned due to the lack of entanglement and poor signal-to-noise ratio. The first superconducting quantum computer was developed experimentally in 1999, and since 2006 there is a number of new technologies like ion traps, quantum dots, photonic qubits.

IBM has long history of research in superconductors (dating from 1960s), so it was quite easy to implement it for the quantum computing and substantially improve it over the years, so superconductors are currently a very promising technology and we may also say the state of the art for qubit computations.

Quantum Theory

So, what does the quantum theory say? And what is “quantum” actually? Let’s first clarify the terminology.

Theory is an explanation of a certain behavior. And quantum theory is an explanation of quantum behavior of elementary particles like electrons and photons. These particles have properties like position or speed that occur only in discrete quantities (or quanta, which is plural of quantum) but observations have demonstrated that it is impossible to fully and simultaneously determine both of these properties. If we know precisely the position of a particle, we don’t know its speed, and vice versa.

From the point of view of quantum computing, it relies on these three quantum properties or phenomena:

First is superposition. Particle like electron can have spin up or spin down , but its spin can also be in a completely undetermined state, in which we can speak only of possibility that its spin is up and a possibility that at the same time its spin is down.
Second is that the electron can stay in this undetermined, superposition state all until we actually measure it to learn about its property. By the very action of measurement its superposition state disappears and its state becomes determined (spin up or spin down). Observation of the particle of any kind will immediately destroy the superposition, if there was any.
Third property is entanglement. Two electrons can be brought in a state where their behavior is completely correlated regardless of the distance between them.

Quantum theory explains these quantum properties and how these phenomena occur, but why they occur remains a mystery.

Quantum Mechanics is the term very often used in the literature. In most cases it has the same meaning as quantum theory or quantum physics, but there is a subtle difference. Quantum mechanics is a mathematical framework, which is used to explain quantum phenomena. It is a complex and abstract field of mathematics based on linear algebraic operators, vector spaces and complex numbers.

Qubits

The simplest quantum system, and also one which is predominantly used in the quantum computation is qubit. The name is actually an abbreviation of quantum bit. Bit can store only one of the two values (0 or 1). A qubit has a two-dimensional state space and can represent not only these simple states like 0 or 1, but also the superposition state (a linear combination of two states). This allows keeping much more information in a computer memory than it is possible with classical computers. With n qubits we can store $2^{n}$ bits. With 50 qubits, we can store 1’125’899’906’842’624 bits ! And we can manipulate with this information in a quite parallelized way. This is the power of quantum computing.

Apart from logical representation of the information, qubit can also be considered to be a physical quantum system with two basis states, which we manipulate in different ways to perform computations. Electrons or photons with their spins and polarizations are the simplest and smallest ones, but larger systems like trapped ions or superconducting circuits can also be used as qubits. These systems offer advantages that we can better control them, so our operations are more reliable.

It is worth mentioning that besides qubits, there are other multidimensional quantum systems or d-level qudits. These systems can have multiple basis states, not only 0 or 1 , but 0, 1, 2 etc until d. Some successful small-scale implementations of qutrits (d = 3) were realized experimentally based on trapped ions and superconductors. Qutrit is represented by three energy levels, and superposition is created by exciting base energy level of this system to the two higher levels simultaneously with two microwave resonators or two laser beams. As the result, the superposition state will be linear combination of three basis states, not two like with qubits. The main advantage of qudits is that they can encode information beyond binary systems, representing much more different states simultaneously – $d^{n}$ . Qutrits could allow for example much more robust quantum cryptography protocols. Still at present, much more work is being done with qubits. Qudits are in a very early experimentation and much work and improvements will be needed to make them more reliable and manageable. But it is maybe one of the next steps in the evolution of quantum computation.

So, to put this in the context of quantum computation, a quantum computer will use qubits (physical systems) to initialize their states to the value of computational inputs, it will perform a sequence of manipulations (or gate operations) on these physical systems according to a program designed by a quantum programmer, and will produce the altered states of qubits as outputs. In the end, our algorithm will measure this final state of the qubits in order to collect the value of outputs in a form of a classical bitstring.

How do we write and visualize quantum states ?

There are several ways to write the quantum state (let’s call it $\psi$ ) and the most common is with bra-ket notation invented by Paul Dirac, where ‘bra’ (or row-based vector) is written as $\langle\psi|$ and ‘ket’ (or column-based vector) is written as $|\psi\rangle$ . Basis states of one-qubit system are $|0\rangle$ and $|1\rangle$ , and in full vector notation this can be represented as $\begin{bmatrix} 1\\ 0\end{bmatrix}$ and $\begin{bmatrix} 0\\ 1\end{bmatrix}$

Concerning superposition states, its formal definition is that it is a linear combination of basis states, which means that we can write it as:

$|\psi\rangle = \alpha|0\rangle + \beta|1\rangle$

where $\alpha^{2}$ and $\beta^{2}$ represent probabilities for the system to be in states $|0\rangle$ and $|1\rangle$ respectively. As such, $\alpha$ and $\beta$ are subject to the constraint:

$\alpha^{2} + \beta^{2} = 1$

It can be demonstrated that the mathematical representation of the superposition can be also written as:

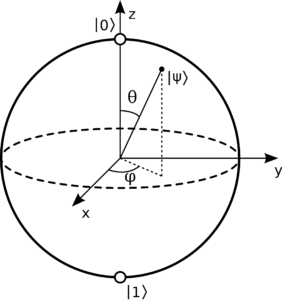
$|\psi\rangle = cos\frac{\theta}{2}|0\rangle + sin\frac{\theta}{2}e^{i\phi}|1\rangle$

Using this equation, we can represent the state $|\psi\rangle$ visually as a vector that points to a point on the surface of a sphere (called Bloch Sphere) and which position is determined by angles $\theta$ and $\phi$ :

Physical Implementations

I have already mentioned that the first quantum computer was built based on nuclear magnet resonance. Nowadays there are different modalities of how a quantum computer can be built. The choice of electrons and photons is closest to the initial experiments that confirmed the existence and nature of quantum phenomena, and development of quantum mechanics, but electrons are very small and difficult to control, and photons are flying and it is difficult to make them interact with each other. That is why practitioners were looking for technologies which can be controlled better.

Currently, photonic systems are a very promising technology, so there are various research groups developing solutions either using atoms as intermediaries of interaction between photons, or time-bin qubits, where a beam is split into two photons and than one photon is delayed through a loop and this creates a two-states quantum system. Or for example, single-photon sources that can produce multiple photons simultaneously and subsequently bring them to entangle with each other.

There is another experimental technology with a lot of potential which is based on tiny artificial diamonds where one carbon atom is mechanically replaced by a silicon. This “defect” imbalance so an electron is trapped in that tiny space, and can be controlled by laser beams. The advantage is that we can establish direct communication with this silicon atom, which allows data input and output, and connections between different diamonds. But the main disadvantage is that placing these artificial atoms on that precise location measured in nanometers is still very difficult.

Microsoft works on topological qubits, based on quasiparticles (called Majorana) represented by a behavior of electrons that travel through semi-conductors. Still, these Majorana qubits exist only in theory and have never been really created.

Much more practical is the technology based on trapped ions. These ions are atoms (usually silicon) with one missing electron. As such, they can be controlled by an electromagnetic fields. They are “trapped” in a magnetic field or in a vacuum chamber and their states and positions are controlled by laser beams. Their main advantage is the stability of the quantum state of ions, but the disadvantage is relatively long time needed for the qubit manipulations.

Superconducting qubits are another technology. Circuits are created with Josephson Junction that will ensure that oscillations within this circuit are anharmonic, which means that the distance between different energy levels is not equal. These circuits are then cooled to the sub-K temperature, which allows the generation and control of the quantum phenomena with microwave pulses directed to this circuit through a resonator. The advantage is that the qubit is always in the same position, can be controlled efficiently and operations on these qubits are very fast. However, superconducting qubits are prone to short coherence times, and as of 2019 this is around 50-70 μs. But, as one single-qubit operation typically takes several ns, this is sufficient to run some experimental algorithms.

Quantum Algorithms

The big idea of developing quantum algorithms (we can call it the quantum algorithm framework) is first to take advantage of quantum superposition, in order to encode exponentially many states in the available qubits of a quantum computer, then exploit entanglement to make it possible to manipulate these large state space simultaneously. Next, we will use quantum operations (called ‘gates’) to evolve the state of this complex quantum system to represent the solution of our real-world problem, and in the end, we will perform readout (or measurement) to extract the result of our computation. Set of basic quantum gates could be written as:

Each of these single-qubit and two-qubit operations (with the exception of measurement) can be visually described as rotation of the vector on the Bloch sphere around one of the three axes: $x$ , $y$ or $z$ . In addition to these simple gates that flip quantum states from one pole to another, we can also use parameterized gates that will do the vector rotation at arbitrary angles: $R_x, R_y, R_z$

Quantum circuits are sequences of quantum gates, that start from the initialization of qubits, and then we will follow the general framework: superposition, entanglement, evolving the states through parameterized rotational gates and in the end the readouts. Readouts will induce the breakout of the superposition where all vectors collapse to the computational basis. This is a stochastic process, which means that the results might be different if we repeat the execution of this circuit several times, because a vector that points to the middle point between the north and south pole of the Bloch sphere at the moment of measurement can collapse with the same probabilities to the north and to the south. And if the vector points closer to the north, the state can still colapse, but more rarely to the south pole. By running the same circuit many times we actually discover the amplitude probabilities and the position of the quantum state vectors before the measurement. It is customary to repeat this experiment 1’000 or 10’000 times, as more repetitions will give us better accuracy in our results.

Use Cases for Quantum Computing

It is expected that quantum computing will help resolve some of the computationally intractable problems for classical computers. Examples are being described in the domains of quantum chemistry (for the simulation of molecules and their interactions), optimization and machine learning.

An example of a problem in chemistry : nitrogen fixation used for the production of fertilizers. It is estimated that 1-2% of world’s energy is spent on Haber-Bosch process, which mixes a metal catalyst with nitrogen and hydrogen at high pressure (200MPa) and temperature of 450 C in order to produce ammonia. There are some enzymes in nature that do this at the room temperature, but it is completely unknown how they are doing it. This is believed to be possible to simulate and understand with quantum computers.

Concerning optimization problems, there are many potentially useful ideas of how to develop quantum algorithms that can help optimize investment portolios, the usage and reallocation of energy flows, logistics and supply chains on both enterprise and global levels.

Machine learning is another potential application domain for quantum computers. Here we talk mostly about using quantum computers to handle classical data coming from the real-world problems (so-called quantum-enhanced machine learning), even though there are some promising use cases for the classical machine learning that can help mitigate quantum noise. This quantum-enhanced machine learning is a large area of intersection between artificial intelligence and quantum computing and many successful experiments have been done to implement linear quantum classifiers, quantum support vector machines, quantum neural networks, or hybrid quantum-classical neural networks, of which I will write in some of the future articles.

Conclusion

This introduction to quantum computing is already by itself a large topic. It includes mathematical, physical, and computational aspects, as well as considerations of potential domains of application. Quantum computing (and quantum technologies in general) will enable breakthrough innovations, but as of 2019/2020 they are still at the early stage of development. My recommendation is to learn about it in order to understand how it may impact your own profession and the timeline of these effects. If you are investor, you might like to understand what companies and technologies are promising, where they are now, and what should be your investment horizon. If you work as computer scientist, you might be interested to know what problems can be successfully implemented on quantum computers. If you are pysicist, you might decide to expand your knowledge towards information science.

Personally I find this field extremely exciting.

Sasha Lazarevic
September 2019